求め方は,<時間─速さ>のグラフから<時間─距離>のグラフを導いたやり方と同じである。 すなわち,つぎの「近似の精度を上げていく」を実行する: 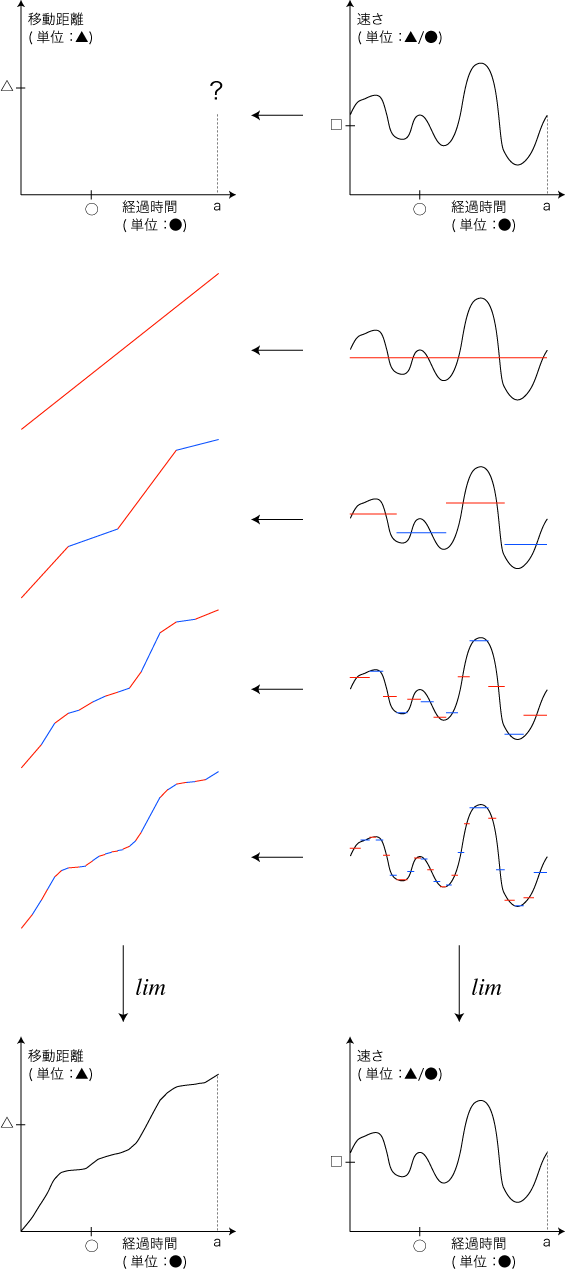
この手順を,式に表現してみる。 k番目の近似になるところの階段グラフを,Gk とする。 Gk において,各階段の幅の値と速さの値を,Δtk,vk (k=1, ‥‥, n) とするとき,Gk に対応する<時間─距離>の折れ線グラフのaにおける値は,つぎの式で求められる:
あるいは,∑ (シグマ) の記号を用いて:
そこで,「時間の区分を細かくする」によって近似の精度を上げていったときの極限は,lim の記号を用いたつぎの式になる:
|