<時間─速さ>を関数f: D → 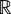 (D ⊂ (D ⊂ 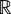 ) と区間 [a, b] ⊂ D の話に一般化するとき,上の式に対応する内容はつぎのようにになる: ) と区間 [a, b] ⊂ D の話に一般化するとき,上の式に対応する内容はつぎのようにになる:
- fは,ある関数F: D →
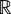 とつぎのように関係している: とつぎのように関係している:
各x∈D に対し,f(x) はFのxにおける変化率。
(すなわち,fはFの導関数。)
- 区間 [a, b] におけるFの増分を,fを用いて求めることを考える。
その方法として,区間 [a, b] の区分
a = x1 < x0 < ‥‥ < xn-1 < xn = b
Δxk = xk+1 - xk (k= 1, ‥‥, n-1)
に対するつぎの式を,求める値の近似式と見る:
そして,この式を「fを区間 [a, b] において区分求積する」と読む。
「求積」の用語の根拠は,「増分を少しずつ積むやり方で,全体の増分を求める」の内容になっているからである。
- この区分を限りなく細かくしていったときの
が,求める全体の増分になる。
|
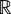 (D ⊂
(D ⊂ 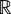 ) と区間 [a, b] ⊂ D の話に一般化するとき,上の式に対応する内容はつぎのようにになる:
) と区間 [a, b] ⊂ D の話に一般化するとき,上の式に対応する内容はつぎのようにになる:
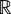 (D ⊂
(D ⊂ 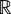 ) と区間 [a, b] ⊂ D の話に一般化するとき,上の式に対応する内容はつぎのようにになる:
) と区間 [a, b] ⊂ D の話に一般化するとき,上の式に対応する内容はつぎのようにになる: