Up ＜時間─距離＞＜時間─速さ＞の相互導出を問題化 作成: 2010-10-25
更新: 2010-10-26

    ここに，移動する物体ががある。
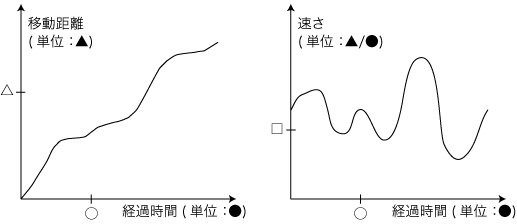
    この移動の記述として，つぎの２つを考える：
    1. 経過時間に対するこれまでの移動距離を記録していく
    2. 経過時間に対するそのときの速度を記録していく
    ここで問題：この二つの記述はどんな関係にあるだろうか？

    どうしてこの問題が出てくるかというと，一方が決まれば他方も決まるように思えるからである。
    実際，経過時間に対する移動距離に違いの現れる箇所でてきたら，それは速さが違う箇所ということになる。 また，経過時間に対する速さに違いの現れる箇所がでてきたら，それは移動距離が違う箇所ということになる。
    そして，一方が決まれば他方も決まるということは，一方から他方を導く方法があるということではないか？

    実際，この予想は正しい：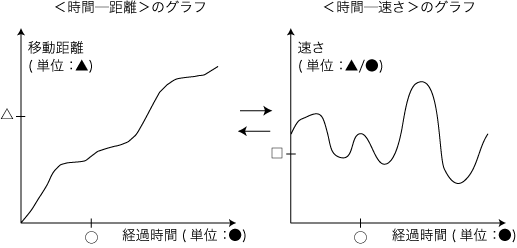
    • ＜時間─距離＞から＜時間─速さ＞を導くことができる
    • ＜時間─速さ＞から＜時間─距離＞を導くことができる
    このことを，ここでつぎのように表現する：
    • ＜時間─距離＞のグラフから＜時間─速さ＞のグラフを導くことができる
    • ＜時間─速さ＞のグラフから＜時間─距離＞のグラフを導くことができる



    さて，＜時間─距離＞と＜時間─速さ＞の一方から他方を導く方法とは？



    註：＜時間─距離＞, ＜時間─速さ＞のグラフを描く手順

    1. 時間，距離の単位を定める──それぞれ●，▲とする。
      速さの単位を，▲/● に定める。

    2. グラフの枠となる時間，距離，速さの軸を描く。


    3. 「枠のスケールを定める」こととして，時間，距離，速さの各軸に適当な数値をおく──それぞれ○，△，□とする。


    4. この枠にしたがって，＜時間─距離＞，＜時間─速さ＞のデータをプロットする。



    「時間，距離，速さの軸を描きこれのスケールを定める」でやっていることは，＜量＞としての時間，距離，速さのそれぞれで，＜量＞としての長さと「同型 (isomorphism)」を立てるということである。