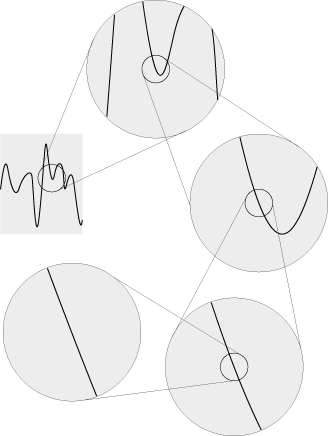
これは,aの近傍では速さvの等速運動になっているということを意味する。 そしてこれは,<時間─距離>のグラフがaにおいて「局所的に線形」ということである。 「局所的に線形」は,連続であって角(かど)がない状態,すなわち「なめらか」な状態である。 「なめらか」は,「局所的に線形」の意味で数学用語になっている。
|
| Up | 「速さがある」: 運動がなめらか (局所的に線形) | 作成: 2010-10-25 更新: 2010-10-25 |
これは,aの近傍では速さvの等速運動になっているということを意味する。 そしてこれは,<時間─距離>のグラフがaにおいて「局所的に線形」ということである。 「局所的に線形」は,連続であって角(かど)がない状態,すなわち「なめらか」な状態である。 「なめらか」は,「局所的に線形」の意味で数学用語になっている。

|