- 「平行」の意義は「同方向」です。
実際,「平行」の意義を「交わらない」にすると,これは実現できるものではありません。
「同方向」は,つぎのように実現します(註):
- 「同方向」からは,「交わらない」の意味の「平行」が導かれます(註)。
- なお,「同方向」のときには,「直線間の距離」を考えることが可能になります。
──「直線間の距離」を考えることができるのは,「同方向」の場合です。
| 註 : |
ある角度の同位角でつくった「同方向」は,別の角度の同位角でつくっても「同方向」でなければなりません。
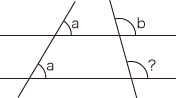
すなわち,つぎの図の ? は b にならなければなりません:
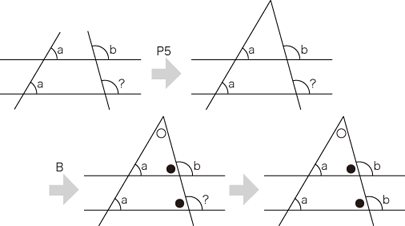
実際,このことは,公準1〜4のもとで,第5公準 P5 と同値になります:
- 公準1〜4+ P5 は,公準1〜4+ P5+「三角形の内角の和は2直角」となり,これより C が導かれる。
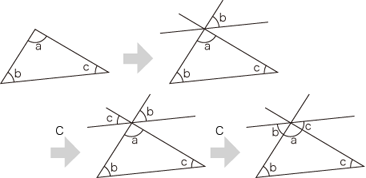
- 逆に,公準1〜4+「一組の同位角が等しければ,任意の組の同位角が等しい」 からは,「三角形の内角の和は2直角」が導かれ,よって P5 が導かれる:
|
|