算数では,自然数と分数の二種類の数を扱う。
中学数学になると「正負の数」という主題名で,整数,有理数の登場となり,さらに「平方根」の主題名で実数が登場する。
高校数学では,実数の主題を進める一方で,あらたに複素数を主題化する。
大学の数学の専門課程では「四元数」の授業があるかも知れない。
これら「数」が「数」の名で一つに括られるのは,これらに同じ<形>が見られているからである。
数学的には,「数」はこの<形>を指すことばである。
- 歴史的には,「「数」の<形>の実現」という意識に導かれていろいろな数がつくられてきたわけではない。歴史はつぎのようになる:
- いろいろな数が,それぞれ何らかの目的に導かれて,つくられる。
- いろいろな数がつくられてきたところで,これらを見渡す。
そこから,共通する<形>が浮かんで見えてくる。
- この形を定式化し,「数」の定義とする。
- 「数」の範疇を拡げるほど,「数」の条件は弱まる。例えば,
- 複素数を考えることで,順序関係は「数」の条件でなくなる。
- 四元数を考えることで,乗法の可換性は「数」の条件でなくなる。
一方,数の使用──特に,量処理における数使用──の根拠となる形式は,「数」の条件として堅持される。
以上のように考えるとき,「数」(自然数,分数,‥‥ といったそれぞれの系) は,およそ(註0)つぎのように定義されるものになる:
「数」とは,集合Nとその上の二つの内算法+,×でなる系 (N,+,×) で,つぎの条件を満たすものである:
- +は結合的かつ可換.
- ×は結合的で,単位元1∈N*が存在する.
- +と×の間に左右分配法則が成り立つ(註1):
a×(b+c)=a×b+a×c
(b+c)×a=b×a+c×a
- 各要素は,+に関して可約;即ち,
a+b=a+c 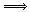 b=c b=c
- N*の各要素は,×に関して左右可約;即ち,a∈N* に対し,
a×b=a×c 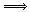 b=c b=c
b×a=c×a 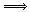 b=c b=c
- 任意の要素a,bに対し,要素cで,a+c=bかa=b+cとなるものが存在する.
|
ここでN*は,Nが零元0── +に関する中立元──をもつときはN\{0} (註2),そうでないときはN自身。
単位元1の存在と条件(4),(5) は,「数使用」の観点から要請される。(N,+) (註3)が群のとき,(4) はこれに含意される。また(N*,×)が群のとき,(5) はこれに含意される。また,×が可換のとき,(3) の条件式は第一式のみでよいことになる。
なお,要素aに対しa+a=aが成り立つとき,aは零元である(註4)。
| (註0) |
「およそ」とここで言っているのは,私見として示しているからである。
|
| (註1) |
「加法」,「乗法」の呼称ないし+,×の記号の使い分けは,それの用法に基づいている (+は倍の和,×は倍の合成に使う)。一方,形式だけを見ると,両者の区別は専ら分配法則に拠っていることになる。即ち,
(x*y)#z=x#z*y#z
の関係にある*の方が加法 (+),#が乗法 (×) となるわけである。
|
| (註2) |
一般に,集合Xとその部分集合Yに対し,Yに属さないXの要素全体の集合をX\Yで表わす。
|
| (註3) |
数の系の構造は,+,×で定義される代数的構造,順序関係≦で定義される順序構造,また位相構造,の組合せで,色々に考えられる。
|
| (註4) |
任意の要素bに対し,a+b=(a+a)+b=a+(b+a)。+の可約性より,b=b+a。
|
|
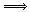 b=c
b=c