Up \( P,\ T \) の \( (S_a, P_a) \) 表現 作成: 2022-10-03
更新: 2022-10-04

    \( (P, \bf{v} ) \) -座標のパラメータとして，\( (S_a, P_a ) \) をつぎのように導入した：
    • \( O \) から \( T \) を見て，\( OQ \) から \( OP \) までの右回転角度を，\( P_a\ ( 0 \leqq P_a < \pi ) \) とする。
    • \( O \) からｘ軸の正の方向を見て，\( ON \) から \( OT \) までの右回転角度を，\( S_a\ ( - \pi < S_a < \pi ) \) とする。
    ここで \( S_a \) の定義における「右回転」「\( S_a\ ( - \pi < S_a < \pi ) \)」の意味は
    　「 \( ON \) から \( OT \) までの右回転角度が \( \pi \) を超え，左回転角度が \( \theta < \pi \) であるときは，\( - \theta \) を \( S_a \) とする」
    である。──これは \( P \) が南半球にある場合。


    \( (S_a, P_a ) \) は，\( P = ( P_x,\ P_y,\ P_z ),\ T = ( 0,\ T_y,\ T_z )\) を表そうとするものである。
    表現式を当て込むために，\( P_x > 0,\ P_y > 0,\ P_z > 0 \) の場合でやってみると：
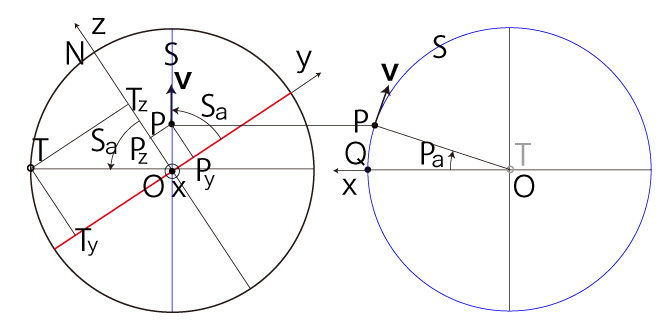
      \[ P_x = R\ cos( P_a ) \\ P_y = ( R\ sin( P_a ) )\ cos( S_a ) \\ P_z = ( R\ sin( P_a ) )\ sin( S_a ) \\ T_y = - R\ sin( S_a ) \\ T_z = R\ cos( S_a ) \\ \]

    この式──以下「＜式＞」と呼ぶ──は，すべての場合で成り立つか？
    以下，これを見ていく。


    先ず，\( P_a = 0 \) は，\( P = Q \) ──即ち \( P_z = 0 \) ──を意味する。
    \( S_a = 0 \) は，S が赤道であること──即ち \( v_z = 0 \) ──を意味する。
    特に，\( S_a = 0 \) は \( P_a = 0 \) を含意する。

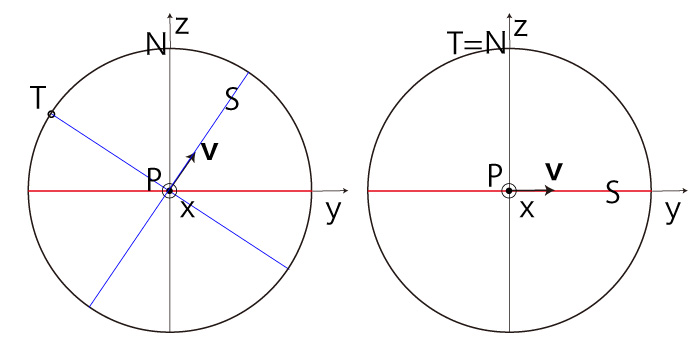
    \( P_z = 0 \) のとき，
      \( v_z = 0 \) (赤道上) ならば
        \( v_y > 0 \) (東向き) ならば \[ P_x = R \\ P_y = ０ \\ P_z = 0 \\ T_y = 0 \\ T_z = R \\ \] \( v_y < 0 \) (西向き) ならば \[ P_x = R \\ P_y = ０ \\ P_z = 0 \\ T_y = 0 \\ T_z = - R \\ \]
    \( v_z > 0 \) (北半球向き) ならば \[ P_x = R \\ P_y = ０ \\ P_z = 0 \\ T_y = - R\ sin( S_a ) \\ T_z = R\ cos( S_a ) \\ \] \( v_z < 0 \) (南半球向き) ならば \[ P_x = R \\ P_y = ０ \\ P_z = 0 \\ T_y = R\ sin( - S_a ) = - R\ sin( S_a ) \\ T_z = R\ cos( - S_a ) = R\ cos( S_a ) \\ \]

    一方，\( P_a = 0 \) のとき，
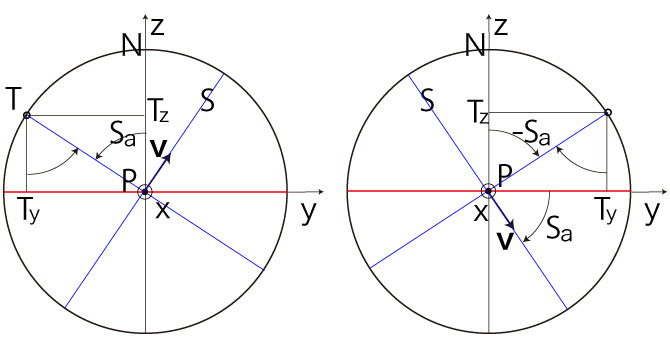
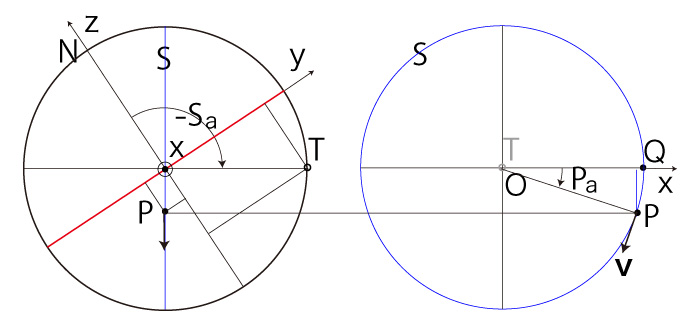
      \[ P_x = R\ cos( 0 ) = R\ cos( 0 ) = R \\ P_y = ( R\ sin( P_a ) )\ cos( S_a ) = ( R\ sin( 0 ) )\ cos( S_a ) = 0 \\ P_z = ( R\ sin( P_a ) )\ sin( S_a ) = ( R\ sin( 0 ) )\ sin( S_a ) = 0 \\ T_y = - R\ sin( S_a ) \\ T_z = R\ cos( S_a ) \\ \]

    よって，＜式＞は \( P_a = 0 \) の場合を含む。


    \( P_z > 0 \) の場合──即ち，\( P \) が北半球にある場合

    \( P_x \geqq 0,\ P_y \geqq 0 \) のとき，

    \( P_x \geqq 0,\ P_y < 0 \) のとき，

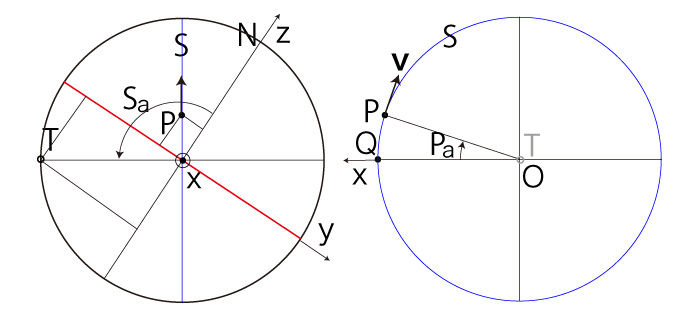
    \( P_x < 0,\ P_y \geqq 0 \) のとき，

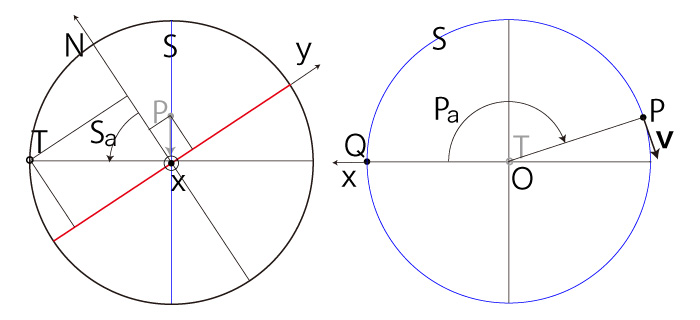
    \( P_x < 0,\ P_y < 0 \) のとき，

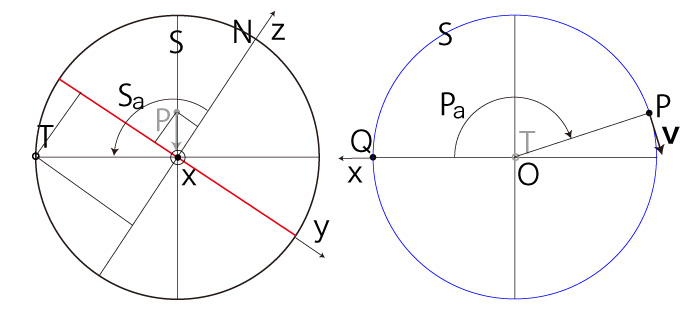
    どの場合も，
      \[ | P_x | = | R\ cos( P_a ) | \\ | P_y | = | ( R\ sin( P_a ) )\ cos( S_a ) | \\ | P_z | = | ( R\ sin( P_a ) )\ sin( S_a ) | | T_y | = | R\ sin( S_a ) | \\ | T_z | = | R\ cos( S_a ) | \\ \]
    ──正負がはっきりしないので，とりあえず絶対値をつけておく。

    \( P_x,\ P_y,\ P_z,\ T_y,\ T_z \) の値の正負は：

0 < Pa < π/2 Pa = π/2 π/2 < Pa< π
Px + 0 -

0 < Sa < π/2 Sa = π/2 π/2 < Sa < π
Py + 0 -
Pz + R +
Ty - -R -
Tz + 0 -

    これに対し，
      \[ | P_x | = | R\ cos( P_a ) | \\ | P_y | = | ( R\ sin( P_a ) )\ cos( S_a ) | \\ | P_z | = | ( R\ sin( P_a ) )\ sin( S_a ) | \\ | T_y | = | R\ sin( S_a ) | \\ | T_z | = | R\ cos( S_a ) | \]
    での
      \[ cos( P_a ) \\ sin( P_a )\ cos( S_a ) \\ sin( P_a ) \ sin( S_a ) \\ sin( S_a ) \\ cos( S_a ) \]
    の正負は：
0 < Pa < π/2 Pa = π/2 π/2 < Pa< π
cos( Pa ) > 0 cos( Pa ) = 0 cos( Pa ) < 0
cos( Pa ) + 0 -

    そして \( sin( P_a ) > 0 \) なので，
0 < Sa < π/2 Sa = π/2 π/2 < Sa < π
cos( Sa ) > 0
sin( Sa) > 0		 cos( Sa ) = 0
sin( Sa) = 1		 cos( Sa ) < 0
sin( Sa) > 0
sin( Pa ) cos( Sa ) + 0 -
sin( Pa ) sin( Sa ) + 1 +
sin( Sa ) + 1 +
cos( Sa ) + 0 -

    したがって，
      \[ P_x = R\ cos( P_a ) \\ P_y = ( R\ sin( P_a ) )\ cos( S_a ) \\ P_z = ( R\ sin( P_a ) )\ sin( S_a ) \\ T_y = - R\ sin( S_a ) \\ T_z = R\ cos( S_a ) \]

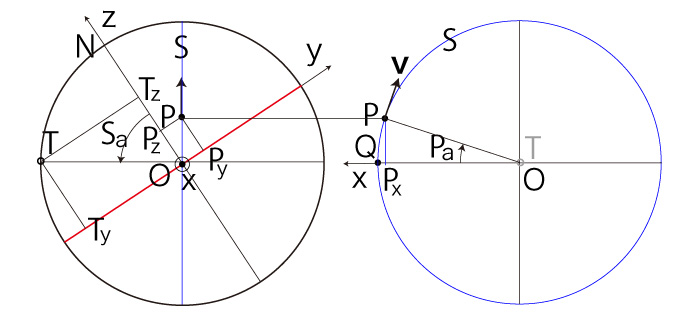
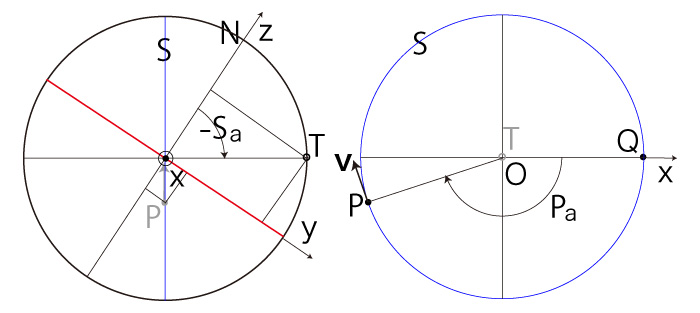
    即ち，＜式＞は \( P_z > 0 \) の場合 の場合を含む。


    \( P_z < 0 \) の場合──即ち，\( P \) が南半球にある場合

    \( P_x \geqq 0,\ P_y \geqq 0 \) のとき，
    \( P_x \geqq 0,\ P_y < 0 \) のとき，
    \( P_x < 0,\ P_y \geqq 0 \) のとき，
    \( P_x < 0,\ P_y < 0 \) のとき，


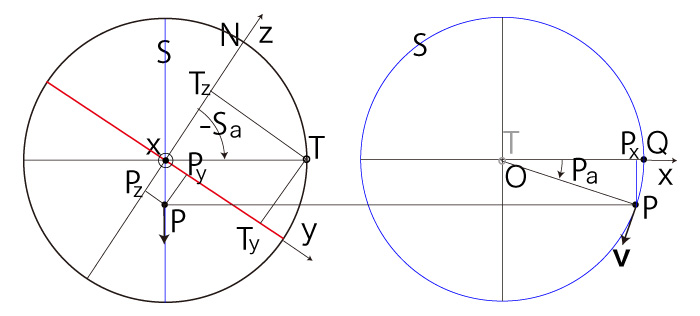
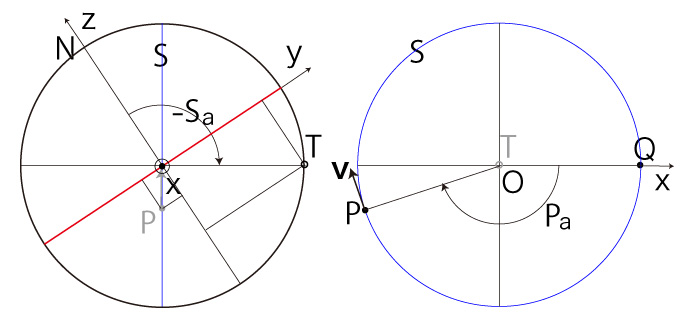
    \( P_x,\ P_y,\ T_y,\ T_z \) の値の正負は：

0 < Pa < π/2 Pa = π/2 π/2 < Pa< π
Px + 0 -

0 > Sa > -π/2 Sa = -π/2 - π/2 > Sa > -π
Py + 0 -
Pz - - R -
Ty + R +
Tz + 0 -

    このとき，
      \[ | P_x | = | R\ cos( P_a ) | \\ | P_y | = | ( R\ sin( P_a ) )\ cos( - S_a ) | = | R\ sin( P_a )\ cos( S_a ) | \\ | P_z | = | ( R\ sin( P_a ) )\ sin( - S_a ) | = | R\ sin( P_a )\ sin( S_a ) | \\ | T_y | = | R\ sin( - S_a ) | = | R\ sin( S_a ) | \\ | T_z | = | R\ cos( = S_a ) | = | R\ cos( S_a ) | \]
    での
      \[ cos( P_a ) \\ sin( P_a )\ cos( S_a ) \\ sin( P_a ) \ sin( S_a ) \\ sin( S_a ) \\ cos( S_a ) \]
    の正負は：
0 < Pa < π/2 Pa = π/2 π/2 < Pa< π
cos( Pa ) > 0 cos( Pa ) = 0 cos( Pa ) < 0
cos( P_a ) + 0 -

    そして \( sin( P_a ) > 0 \) なので，
0 > Sa > -π/2 Sa = -π/2 - π/2 > Sa > -π
cos( Sa ) > 0
sin( Sa) < 0		 cos( Sa ) = 0
sin( Sa) = -1		 cos( Sa ) < 0
sin( Sa) < 0
sin( Pa ) cos( Sa ) + 0 -
sin( Pa ) sin( Sa ) - -1 -
sin( Sa ) - -1 -
cos( Sa ) + 0 -

    したがって，
      \[ P_x = R\ cos( P_a ) \\ P_y = R\ sin( P_a )\ cos( S_a ) \\ P_z = R\ sin( P_a )\ sin( S_a ) \\ T_y = - R\ sin( S_a ) \\ T_z = R\ cos( S_a ) \]

    即ち，＜式＞は \( P_z < 0 \) の場合を含む。


    まとめ
      \[ P_x = R\ cos( P_a ) \\ P_y = R\ sin( P_a )\ cos( S_a ) \\ P_z = R\ sin( P_a )\ sin( S_a ) \\ T_y = - R\ sin( S_a ) \\ T_z = R\ cos( S_a ) \\ \]