\( ( P, \bf{v} ) \) から \( \Delta t \) 後の位置 \( P' \) は,\( ( P, \bf{v} ) \)-大円 \( S \) 上を \( \bf{v} \) の方向に距離 \( | {\bf{v}} |\ \Delta t \) だけ進んだところである。
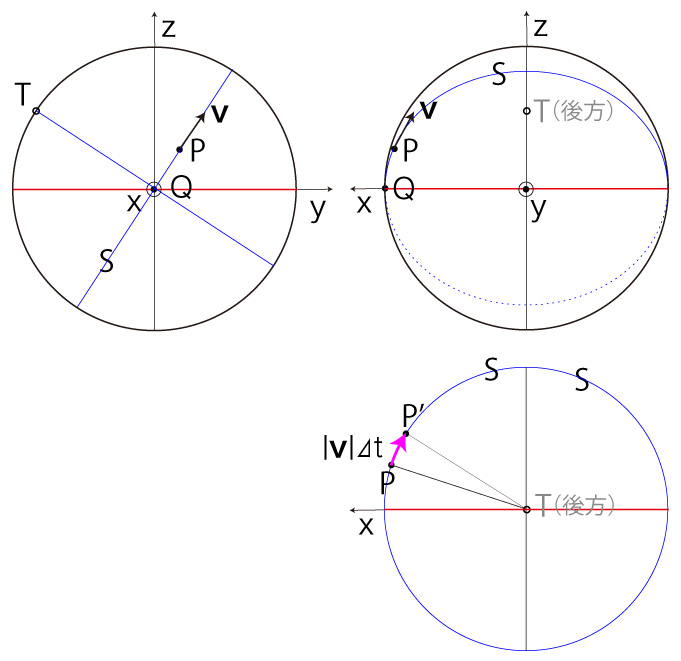
つぎのようにおく:
\[
P = ( P_x,\ P_y,\ P_z ) \\
v = | {\bf{v}} | \\
\ \\
P' = ( P'_x,\ P'_y,\ P'_z ) \\
\]
以下,\( P'_x,\ P'_y,\ P'_z \) を求める。
\( P'_x,\ P'_y,\ P'_z \) は,つぎの図に示される:
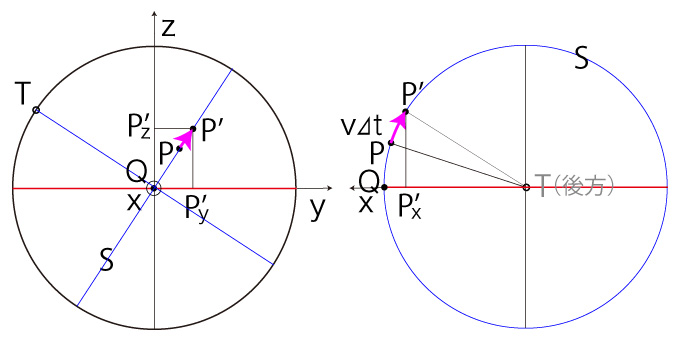
ここで回転角 \( S_a,\ P_a,\ \theta \) をつぎのようにとる :
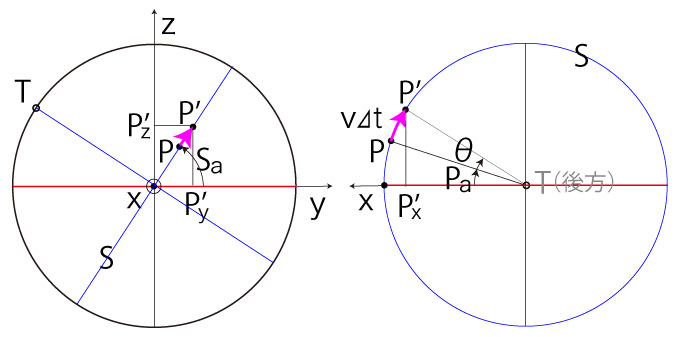
このとき
\[
v\ \Delta t = R\ \theta
\]
\[
\begin{align}
P'_x = & R\ cos( P_a + \theta ) \\
= & R\ ( cos( P_a )\ cos( \theta ) - sin( P_a )\ sin( \theta ) ) \\
= & R\ \bigl( cos( P_a )\ cos( \frac{ v\ \Delta t }{ R } ) - sin( P_a )\ sin( \frac{ v\ \Delta t }{ R } \bigr) \bigr)
\end{align}
\]
そして,図
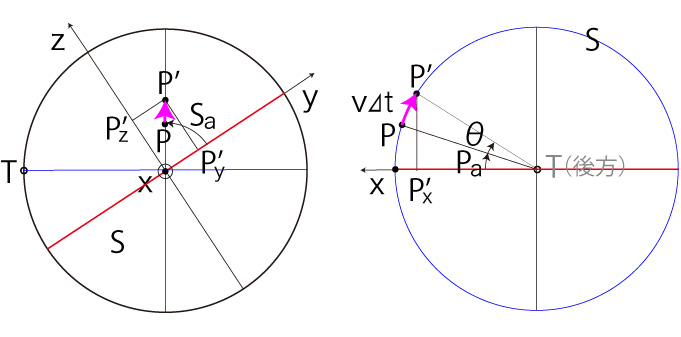
は,つぎの関係を示す:
\[
P'_y = ( R\ sin( P_a + \theta ) )\ cos( S_a ) \\
P'_z = ( R\ sin( P_a + \theta ) )\ sin( S_a ) \\
\]
よって,
\[
\begin{align}
P'_y & = R\ ( sin( P_a )\ cos( \theta ) + cos( P_a )\ sin( \theta ) )\ cos( S_a ) \\
& = R\ cos( S_a )\ \bigl( sin( P_a )\ cos( \frac{ v\ \Delta t }{ R } ) + cos( P_a )\ sin( \frac{ v\ \Delta t }{ R } ) \bigr)\ \\
P'_z & = R\ sin( S_a )\ \bigl( sin( P_a )\ cos( \frac{ v\ \Delta t }{ R } ) + cos( P_a )\ sin( \frac{ v\ \Delta t }{ R } ) \bigr)\ \\
\end{align}
\]
\( cos( S_a ),\ sin( S_a ),\ cos( P_a ),\ sin( P_a ) \) は,\( P \) の座標によってつぎのように表された:
(1) \( P_x = R,\ P_y = P_z = 0,\ v_x = v_z = 0 \) の場合
── \( S \) が赤道の場合
\[
cos( S_a ) = 1 \\
sin( S_a ) = 0 \\
cos( P_a ) = 1 \\
sin( P_a ) = 0 \\
\]
(2) \( P_y = 0,\ v_y = 0 \) の場合
── \( S \) が経線の場合
\[
cos( S_a ) = 0 \\
sin( S_a ) =
\begin{cases}
1 & ( P_z > 0 ) \\
-1 & ( P_z < 0 ) \\
\end{cases}
\\
cos( P_a ) = \frac{ P_x }{ R } \\
sin( P_a ) = \frac{ P_z }{ R } \\
\]
(3) \( P_x = R,\ P_y = P_z = 0 \) の場合
── \( P \) が赤道上にある場合
\[
cos( S_a ) = R\ \frac{ v_y }{ v } \\
sin( S_a ) = R\ \frac{ v_z }{ v } \\
cos( P_a ) = 1 \\
sin( P_a ) = 0 \\
\]
(4) 上のいずれでもない場合
\[
cos( S_a ) = \frac{ P_y }{ \sqrt{ R^2 - P_x^2 } } \\
sin( S_a ) = \frac{ P_z }{ \sqrt{ R^2 - P_x^2 } } \\
cos( P_a ) = \frac{P_x }{R } \\
sin( P_a ) = \frac{ \sqrt{ R^2 - P_x^2 } }{ R } \\
\]
よって,つぎのようになる:
(1) \( P_x = R,\ P_y = P_z = 0,\ v_x = v_z = 0 \) の場合
── \( S \) が赤道の場合
\[
P'_x = R\ cos\bigl( \frac{ v\ \Delta t }{ R } \bigr) \\
P'_y = R\ sin\bigl( \frac{ v\ \Delta t }{ R } \bigr) \\
P'_z = 0
\]
(2) \( P_y = 0,\ v_y = 0 \) の場合
── \( S \) が経線の場合
\[
P'_x = P_x\ cos\bigl( \frac{ v\ \Delta t }{ R } \bigr)
- P_z\ sin\bigl( \frac{ v\ \Delta t }{ R } \bigr) \\
P'_y = 0 \\
P'_z = P_z\ cos\bigl( \frac{ v\ \Delta t }{ R } \bigr)
+ P_x\ sin\bigl( \frac{ v\ \Delta t }{ R } \bigr)
\]
(3) \( P_x = R,\ P_y = P_z = 0 \) の場合
── \( P \) が赤道上にある場合
\[
P'_x = R\ cos( \frac{ v\ \Delta t }{ R } ) \\
P'_y = R\ \frac{ v_y }{ v }\ \bigl( sin( \frac{ v\ \Delta t }{ R } ) \bigr)\ \\
P'_z = R\ \frac{ v_z }{ v }\ \bigl( sin( \frac{ v\ \Delta t }{ R } ) \bigr)\ \\
\]
(4) 上のいずれでもない場合
\[
P'_x = P_x\ cos\bigl( \frac{ v\ \Delta t }{ R } \bigr)
- \sqrt{ R^2 - P_x^2 }\ sin\bigl( \frac{ v\ \Delta t }{ R } \bigr) \\
P'_y = P_y\ cos\bigl( \frac{ v\ \Delta t }{ R } )
+ \frac{ P_x\ P_y }{ \sqrt{ R^2 - P_x^2 } }\ sin\bigl( \frac{ v\ \Delta t }{ R } \bigr) \\
P'_z = P_z\ cos\bigl( \frac{ v\ \Delta t }{ R } )
+ \frac{ P_z\ P_x }{ \sqrt{ R^2 - P_x^2 } }\ sin\bigl( \frac{ v\ \Delta t }{ R } \bigr) \\
\]
|




 計算
計算