これは間違いである。 風は,等圧線に沿う格好で流れる: |
(高層 500hPa 面天気図──Windy.com から引用)
|
元画像はカラーだが,等高線が見えやすいようにグレーに変換
風の流れを示す矢線がこの図ではよく見えない (画像をクリックして拡大表示へ) |

気象学が「風は気圧の高いところから低いところに流れる」と教えるのは,気象学のアタマが「風は気圧が元」──風は結果で気圧が原因──だからである。 しかしこの教えに順えば,風は等圧線と直交するように流れることになる。 実際はそうではないので,気象学は「コリオリ力」「地衡風」といった珍妙な理屈を捻り出す。 しかもたちの悪いことに,その謂うところの「コリオリ力」は,「コリオリ力」の別物化なのである。
気象学は「コリオリ力」教の 「気圧」は,「空気粒子の密度」である。 よって,風は密度を運んでいることになる。 風の流線が,そのまま等圧線になる。 「気圧」はまた,空気の押し合いへし合いの圧である。 したがって,風と気圧は分けられない。 そして「風の流線が,そのまま等圧線になる」のだから,因果を強いて言えばつぎのようになる:
ただし,これは大局観である。 風の中では,密度 (気圧) が絶えず変化している。 例えば,風の幅が狭められるところは,密度が大きくなる──そして風速が大きくなる。
ちなみに等圧線は,等温線がこれとほぼ対応することになる。 空気の流れは,その空気の温度の流れだからである: |
earth.nullschool.net から引用 :
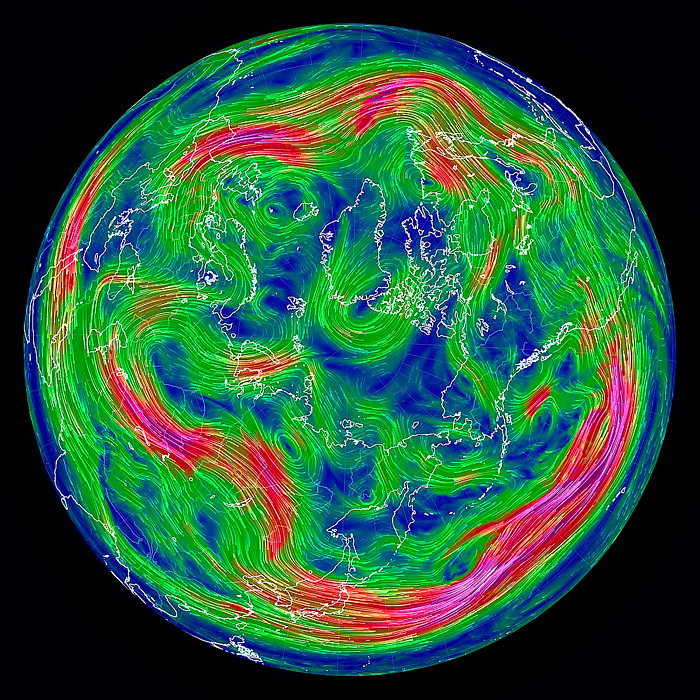



 「日々の気温を大局的に理解する法」
「日々の気温を大局的に理解する法」