──原点を通り,向きが q = (qx, qy, qz) の有向直線 L の回りの θ の回転は,つぎの写像になります (  回転の計算に四元数が使える): 回転の計算に四元数が使える):
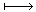 (v'x, v'y, v'z) (v'x, v'y, v'z)
ただし,v'x, v'y, v'z は,つぎの計算で求められる数: M(q, θ) = cos(θ/2) + (qx sin(θ/2)) i + (qy sin(θ/2)) j + (qz sin(θ/2)) k  (q, θ) = cos(ーθ/2)
+ (qx sin(ーθ/2)) i
+ (qy sin(ーθ/2)) j
+ (qz sin(ーθ/2)) k (q, θ) = cos(ーθ/2)
+ (qx sin(ーθ/2)) i
+ (qy sin(ーθ/2)) j
+ (qz sin(ーθ/2)) k
M(q, θ) × (vx i + vy j +vz k) ×  (q, θ)
=
v'x i
+ v'y j
+v'z k (q, θ)
=
v'x i
+ v'y j
+v'z k
ここでつぎのことが問題になります:
答えは「Yes」です。 (  付録 :「回転の合成は回転になる」での計算省略部分) 付録 :「回転の合成は回転になる」での計算省略部分)
|